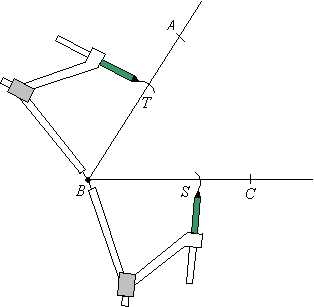
Jmap Angle Bisector

Jmap Angle Bisector. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment's endpoints. The intersection of the perpendicular bisectors of the sides of a triangle is the center of the inscribed circle. DB ≅ EB (CPCTC); AD ≅ CE (segment subtraction);. The intersection of the angle bisectors of a triangle is the center of the circumscribed circle. Please support JMAP by making a donation! Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Angle Side Relationship: Midsegments: Medians, Altitudes and Bisectors: Centroid, Orthocenter, Incenter and Circumcenter: Triangles in the Coordinate Plane: G. Line segments AC, DB, and FG intersect at E.

Jmap Angle Bisector. Line segments AC, DB, and FG intersect at E. Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). In geometry, we usually divide a triangle and an angle by a line or ray which is considered as an angle bisector. Within a given triangle, there are many theorems involving bisectors, medians, and altitudes. Prove theorems about lines and angles. Jmap Angle Bisector.

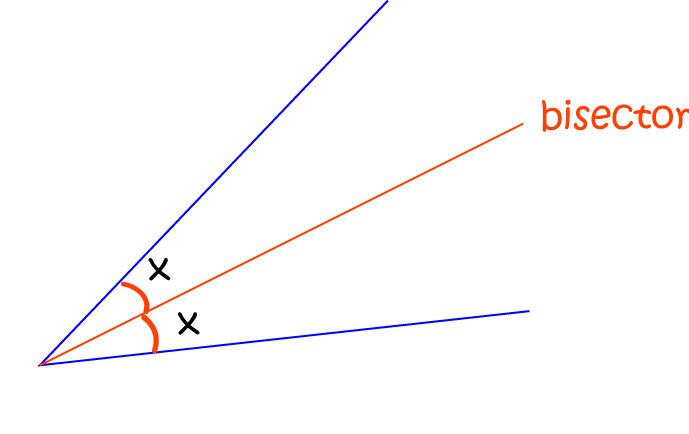
Since a bisector divides a segment into two congruent segments at its midpoint, BC ≅EC.

DB ≅ EB (CPCTC); AD ≅ CE (segment subtraction);.

Angle Bisector | ClipArt ETC

in the given figure , bisectors AP and BQ of the alternate interior …

Angle Bisector (with worked solutions & videos)

MathCamp321 – Geometry: Angle Bisectors – YouTube

Angle bisector-Definition & Examples – Cuemath

What is a bisector – Math – Practical Geometry – 610566 | Meritnation.com

Construct a Perpendicular Bisector of a Line Segment | Interior and …

Construct: Construct The Angle Bisector

Proof: The Angle Bisector Theorem Converse – YouTube

Definition of Angle Bisector – Math Definitions – Letter A

Angle Bisector – YouTube

Angle bisector of a triangle – Mathematical Way

Jmap Angle Bisector. ABE ≅ CBD (given); ∠A ≅ ∠C (CPCTC); ∠AFD. ≅ ∠CFE . (vertical angles are congruent); . ABC, D is a point on AC such that BD is a median. Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Angle Side Relationship: Midsegments: Medians, Altitudes and Bisectors: Centroid, Orthocenter, Incenter and Circumcenter: Triangles in the Coordinate Plane: G. Angle Bisector and Perpendicular Bisector Theorem.

Jmap Angle Bisector.