Umap Analysis. UMAP (Uniform Manifold Approximation and Projection) is a novel manifold learning technique for dimension reduction. It is similar to PCA (Principal Component Analysis) in terms of speed and resembles tSNE to reduce dimensionality while preserving as much information of the dataset as possible. This article will discuss how the algorithm works in practice. The algorithm is founded on three assumptions about the data The data is uniformly distributed on Riemannian manifold; UMAP is an algorithm for dimension reduction based on manifold learning techniques and ideas from topological data analysis. Uniform Manifold Approximation and Projection (UMAP) is a dimension reduction technique that can be used for visualisation similarly to t-SNE, but also for general non-linear dimension reduction. It provides a very general framework for approaching manifold learning and dimension reduction, but can also provide specific concrete realizations. UMAP is a dimensionality reduction algorithm and a powerful data analysis tool. UMAP is a general purpose manifold learning and dimension reduction algorithm.
Umap Analysis. Here we apply uniform manifold approximation and projection (UMAP), a non-linear dimension reduction. UMAP is constructed from a theoretical framework based in Riemannian geometry and algebraic topology. It is similar to PCA (Principal Component Analysis) in terms of speed and resembles tSNE to reduce dimensionality while preserving as much information of the dataset as possible. Uniform Manifold Approximation and Projection (or UMAP) is a new dimension reduction technique that can be used to visualize patterns of clustering in high-dimensional data. Whereas PCoA performs an eigendecomposition that focuses on linearly preserving the pairwise distances between the samples (global structure), UMAP uses a nonlinear graph construction and embedding method to optimize an. Umap Analysis.
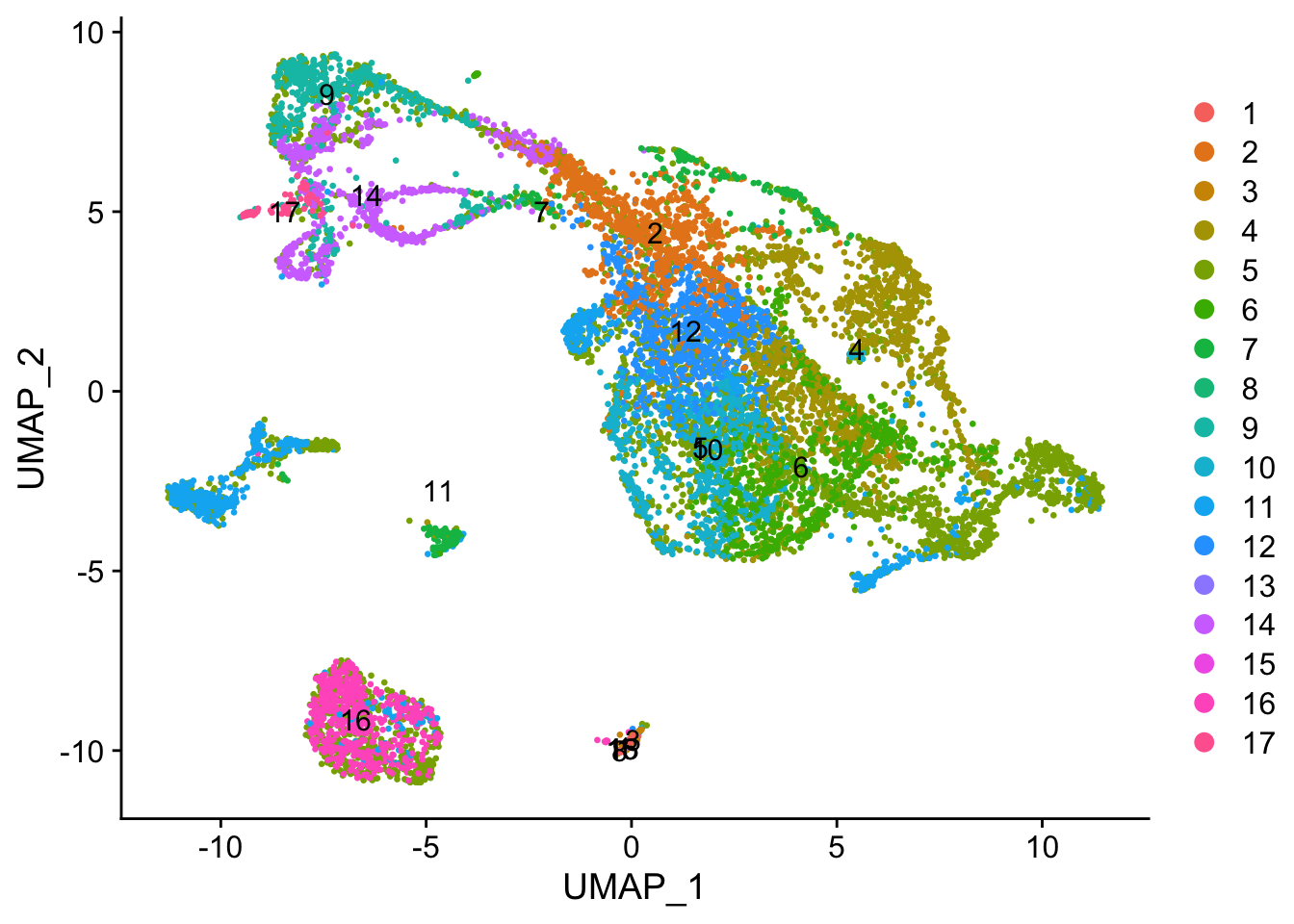
UMAP embedding of the scRNA-seq dataset containing dorsal and ventral.
The following UMAP is my result: And this is the published UMAP: Since the dataset contain smoker and non-smoker data, I played around with the merging sequence, i.e.: merging the data sequentially based on their IDs vs. merging the same type of data first (smoker with smoker and non-smoker with non-smoker) before merging all of them together.
scRNA-seq analysis of CD45+ cells in healthy kidney. (a) UMAP plot …
Single-cell RNA sequencing analysis of midbrain-specific organoids. (a …
Single-cell RNA-sequencing analysis reveals cellular heterogeneity of …
ScRNA-seq identifies CTHRC1โบ pathologic fibroblasts in human fibrotic …
| Single cell sequencing analysis (A). UMAP plot showing 8 cell …
Course: Single cell RNA-seq data analysis with Chipster
Comparative single-cell RNA-sequencing analysis of EpiTS embryoids a …
Pseudotime analysis with slingshot
Lineage progression a, UMAP plot as shown in Fig. 1c, coloured by the …
Basic UMAP Parameters โ umap 0.5 documentation
UMAP representation of dimensionally reduced data following graph-based …
The UMAP Plugin in FlowJo: A User's Review โ The Clambey Lab
Umap Analysis. Its details are described by McInnes, Healy, and Melville and its official implementation is available through a python package umap-learn. UMAP is constructed from a theoretical framework based in Riemannian geometry and algebraic topology. Here we apply uniform manifold approximation and projection (UMAP), a non-linear dimension reduction. Larger values result in more global views of the manifold. Compute the n_neighbors nearest points for each data point in X under metric.
Umap Analysis.